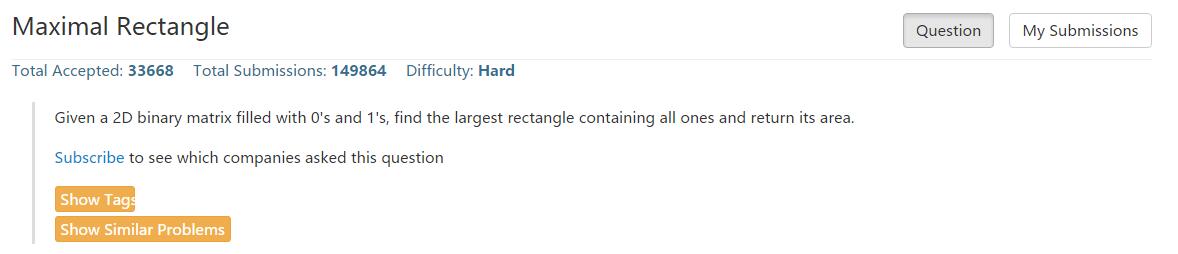
Maximal Rectangle

Problem: Maximal Rectangle

Solve:
解法一：在(i,j)处进行矩形搜索，首先横向搜索，再纵向搜索，搜索方式如下图所示：

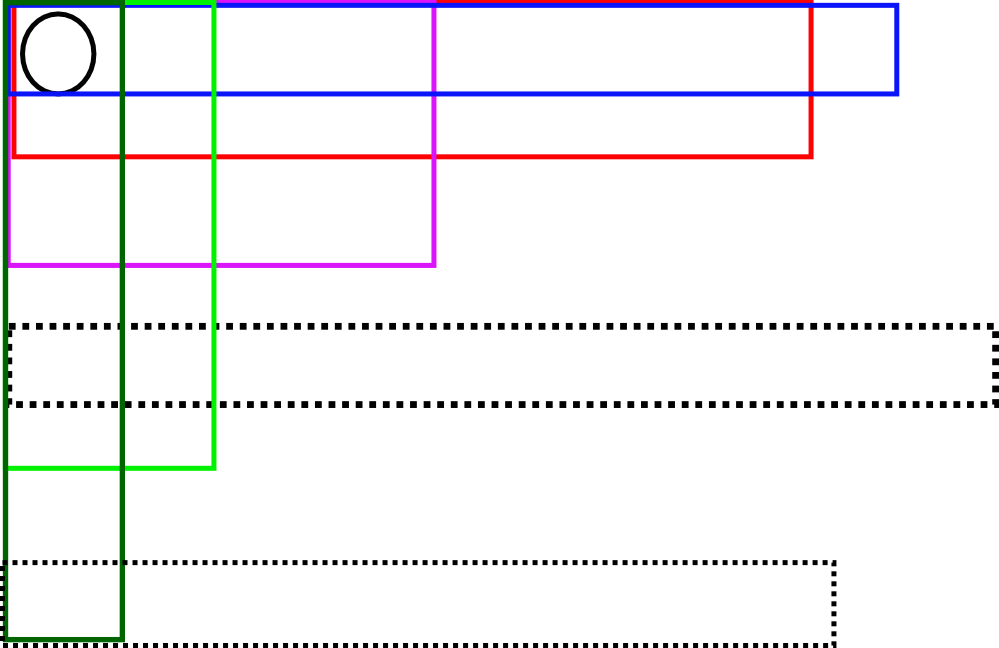
搜索代码如下：
[Java Code]

public int maxRectangle(char[][] matrix, int row, int col) {
        int minWidth = Integer.MAX_VALUE;
        int maxArea = 0;
        for (int i = row; i < matrix.length && matrix[i][col] == '1'; i++) {
            int width = 0;
            while (col + width < matrix[row].length && matrix[i][col + width] == '1') {
                width++;
            }
            if (width < minWidth) {
                minWidth = width;
            }
            int area = minWidth * (i - row + 1);
            if (area > maxArea)
                maxArea = area;
        }
        return maxArea;
    }

然后对矩形中所有点使用上述搜索，就可以找出最大的矩形面积，代码如下：
[Java Code]

public int maximalRectangle(char[][] matrix) {
        int max = 0;
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                max = Math.max(max, maxRectangle(matrix, i, j));
            }
        }
        return max;
    }

解法二：从上往下，按行搜索，每行内容加上它上面的所有行就组成的一个个直方图，所以对每一行而言，都对应一个直方图，所以问题就转换为了求直方图中最大的矩形面积。示意图如下所示：

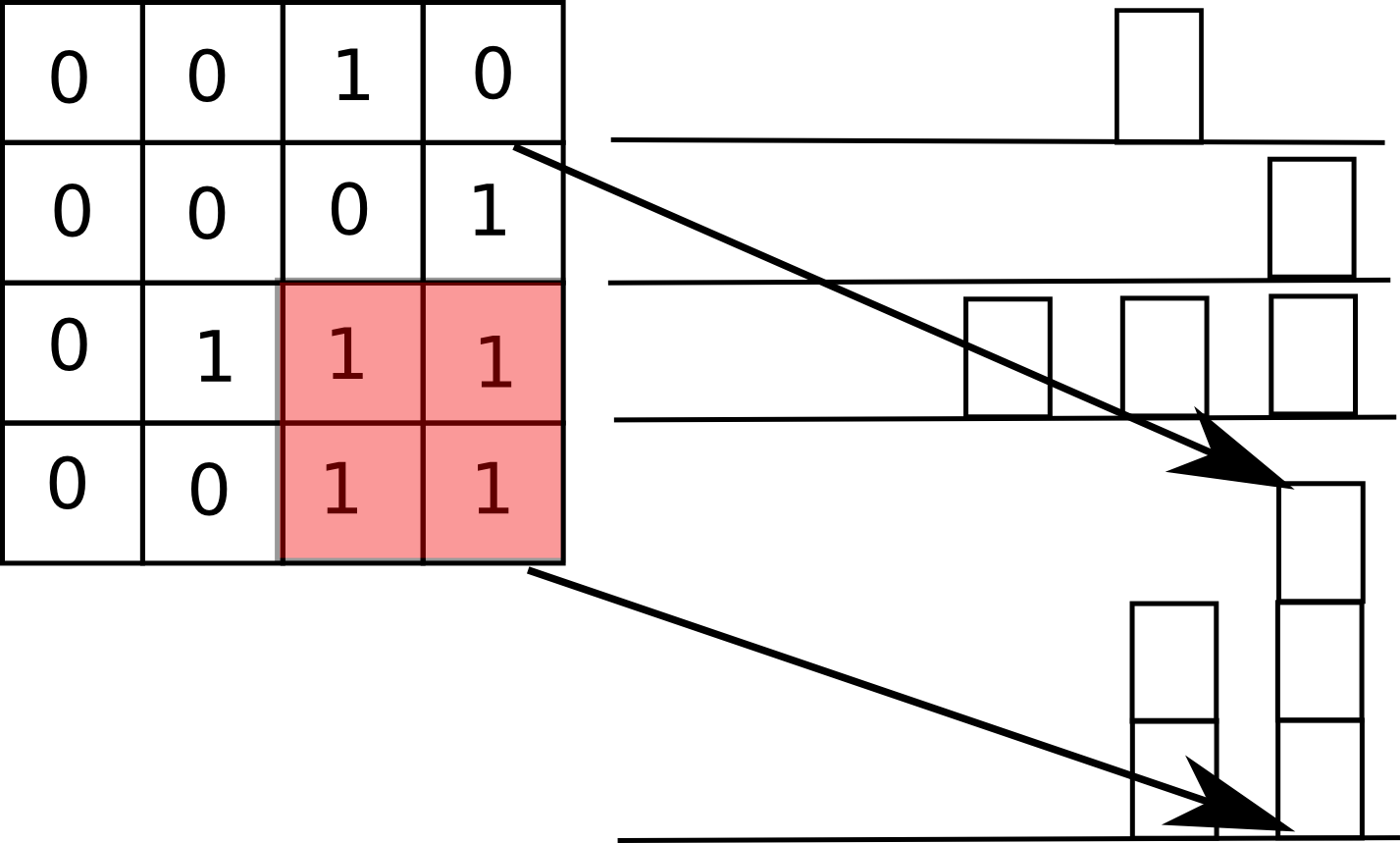
具体讲解请参考直方图博客代码如下所示：
[Java Code]

public int maximalRectangle(char[][] matrix) {
        if (matrix.length == 0 || matrix[0].length == 0) return 0;
        int[] dp = new int[matrix[0].length];
        int max = 0;
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                if (matrix[i][j] == '1') {
                    dp[j] += matrix[i][j] - '0';
                } else {
                    dp[j] = 0;
                }
            }
            max = Math.max(maxRectangle(dp), max);
        }
        return max;
    }

    public int maxRectangle(int[] dp) {
        Deque<Integer> stack = new ArrayDeque<Integer>();
        int n = dp.length, area = 0;
        for (int i = 0; i < n; i++) {
            while (stack.size() > 0 && dp[stack.peek()] > dp[i]) {
                int h = dp[stack.peek()];
                stack.pop();
                int l = stack.size() == 0 ? -1 : stack.peek();
                area = Math.max(area, h * (i - l - 1));
            }
            stack.push(i);
        }
        while (stack.size() > 0 && dp[stack.peek()] > 0) {
            int h = dp[stack.peek()];
            stack.pop();
            int l = stack.size() == 0 ? -1 : stack.peek();
            area = Math.max(area, h * (dp.length - 1 - l));
        }
        return area;
    }

Comments